“Engineering health through the flow of innovation!”

Georgios C. Georgiou is a Professor at the Department of Mathematics and Statistics and Director of the Oceanography Center, University of Cyprus. He has been a research associate at the Université Catholique de Louvain in Belgium, and the Foundation for Research and Technology – Hellas (FORTH) and has taught at various Universities in Greece (Patras, Aegean, Crete), Cyprus (Cyprus University of Technology), Brazil (Universidade Tecnológica Federal do Paraná; Universidade Federal do Rio Grande do Sul), Egypt, and Morocco. His expertise lies in computational rheology, numerical simulations of viscoelastic flows, numerical solution of PDEs, finite element methods, and computational oceanography. Prof. Georgiou has published more than 160 peer-review journal papers and more than 100 papers in conference proceedings. He co-authored two books (Viscous Fluid Flow, CRC Press, 2000; Fluid Mechanics of Viscoplasticity, Springer, 2022). He served as the guest editor of three international rheological journals and as a reviewer in many international scientific journals. In the past 25 years he has been involved as a coordinator or partner in more than 40 national and European research projects. His funded projects range from polymer processing and hemodynamic numerical simulations to oceanographic predictions and tsunami and oil spill modelling.

Professor Georgios C. Georgiou

Department of Mathematics and Statistics

Director, Oceanography Center

University of Cyprus

This email address is being protected from spambots. You need JavaScript enabled to view it.; (+357) 22 892612

My research work mainly concerns the development and the evaluation of numerical methods for solving (i) viscous, viscoplastic or viscoelastic flow problems, with emphasis on free surface, time-dependent compressible flows with or without wall slip and (ii) elliptic boundary value problems, with emphasis on Laplacian and Stokes flow problems involving boundary singularities. In the past few years I have also worked on a number of oceanography projects. I am particularly interested in oceanography projects with numerical, computational, and rheological components. It seems that in many cases, viscoplasticity is relevant in many processes of the ocean and its bottom. In the present brief description, my mathematical research interests as well as some of my CFD interests are excluded.

Computational Fluid Dynamics (CFD)

My early research concerned the solution of free-surface, generalized-Newtonian flow problems with finite elements. I have then worked on the numerical simulation of viscoelastic flows with mixed finite elements using various formulations such as the Galerkin, the streamline-upwinding (SU), and the streamline-upwinding Petrov-Galerkin (SUPG) methods. My current research work concerns the following topics which involve Newtonian, generalized-Newtonian (viscoplastic) and viscoelastic flows. 

1. Simulations of polymer extrusion instabilities
2. Solution of Newtonian flow problems with stress singularities
3. Simulations of steady and time-dependent viscoplastic flows
4. Other compressible flows and flows with pressure-dependent rheological parameters

I have started working on the study of flows where the viscosity is pressure dependent. The long-term objective here is to take the pressure dependence into account together with compressibility and the extension to non-Newtonian flows.

5. Blood flow simulations

6. Flows with wall slip

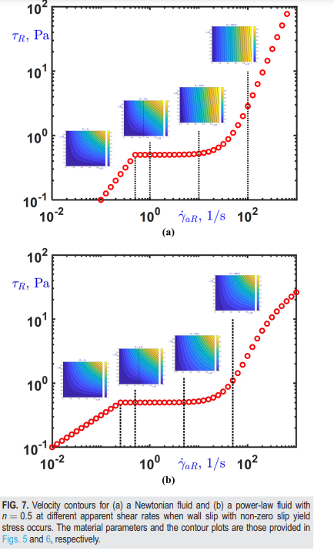
In the past few years, I have studied mostly viscoplastic flows with wall slip. In addition to the standard Navier and power-law-type slip equations, I explored both analytically and numerically the use of equations which predict slip only above a critical wall shear stress, the so-called slip yield stress. We have also proposed and tested a regularized version of this two-branch slip equation which can be easily implemented in existing codes (i.e. finite elements). This work finds applications not only in complex flows but also in micro- and nano-fluidics. It may be also relevant to landslide simulations at the ocean bottom.

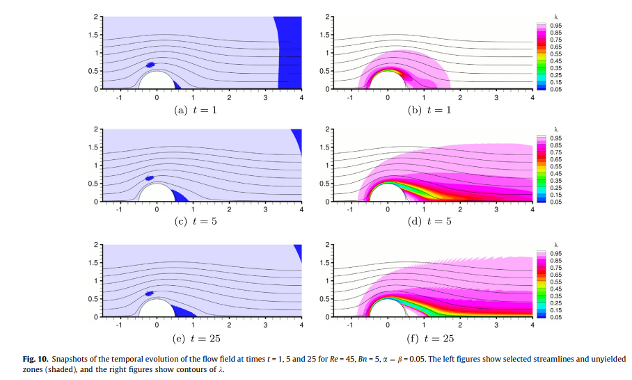
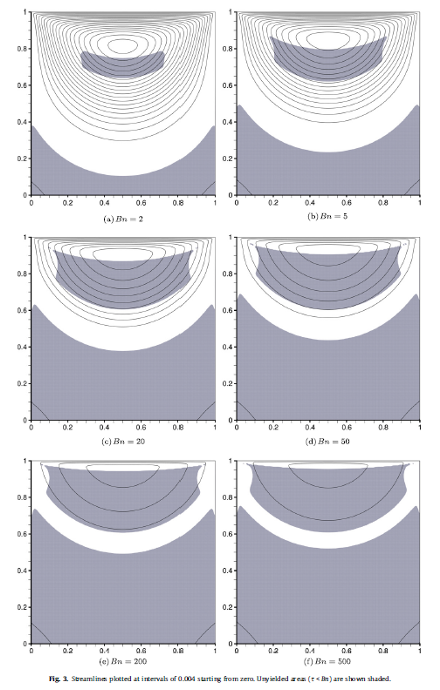
7.   Thixotropic flows

In the past few years, we have developed a thixotropic model. This is a structural viscoplastic model based on the Bingham plastic constitutive equation. The yield stress is assumed to vary linearly with the structural parameter which follows a first-order rate equation accounting for the material structure break-down and build-up. Different flows have already been considered including: (i) flow of semi-solid suspensions in a Couette rheometer; (ii) squeeze flow under either constant load or constant velocity; and (iii) flow of a thixotropic Herschel-Bulkley fluid around a cylinder.

SELECTED GRANTS

1. Erasmus+, 619158-EPP-1-2020-1-CY-EPPKA2-CBHE-JP, ECOMARINE: Building a Comprehensive Mechanism for Preserving Marine Ecosystems and Life from the negative consequences of Climate Change and the disposal of Plastic Debris, 15.1.2021-14.7.2024
2. European Commission. Directorate General, Grant Agreement No. EASME/EMFF/2016/1.2.1.2/06/SI2.749365, Blue Career Centre of Eastern Mediterranean and Black Sea (MENTOR), 1.3.2017-28.2.2019
3. Foundation for the Promotion of Research, Cyprus. The fluidity of blood at different levels of oxygen content, DIAKRATIKES/KY-SLO/0411/02, 1.3.2012-28.2.2014
4. Foundation for the Promotion of Research, Cyprus. Medical Diagnosis Support Tool for Detailed Morphology and Hemodynamic Assessment of the Carotid Bifurcation at Different Head Postures, ΥΓΕΙΑ/ΔΥΓΕΙΑ/0609(ΒΙΕ)/11, 1.3.2011-28.02.2013
5. General Secretariat for Research and Technology, Greece. Image based computational models for patient specific carotid arterial plaque rupture risk estimation, France-Greece, Joint Research and Technology Programmes, 1.2010-31.12.2011

SELECTED PUBLICATIONS

1. Zupančič Valant, L. Ziberna, Y. Papaharilaou, A. Anayiotos, G.C. Georgiou, The influence of oxygen concentration on the rheological properties and flow of whole human blood, Rheol. Acta 55, 921-933 (2016).
2. Dimakopoulos, G. Kelesidis, S. Tsouka, G.C. Georgiou, J. Tsamopoulos, Hemodynamics in stenotic microvessels under steady state conditions. Part I: The non-homogeneous model, J. Biorheology 52(3), 183-210 (2015).
3. Aristokleous, I. Seimenis, G.C. Georgiou, A. Nicolaides, A.S. Anayiotos, The Effect of Head Rotation on the Geometry and Hemodynamics of Healthy Vertebral Arteries, Annals of Biomedical Engineering 43, 1287-1297 (2015).
4. Aristokleous, I. Seimenis, G.C. Georgiou, Y. Papaharilaou, B.C. Brott, A.S. Anayiotos, Impact of head rotation on the individualized common carotid flow and carotid bifurcation hemodynamics, IEEE Journal of Biomedical and Health Informatics 18(3), 783-789 (2014).
5. Zupančič-Valant, M. Lunder, L. Žiberna, Y. Papaharilaou, A. Anayiotos, G. Georgiou, The influence of temperature on rheological properties of blood mixtures with different volume expanders – implications in numerical modelling of arterial hemodynamics simulations, Rheol. Acta 50, 389-402 (2011).